CTF

2025-12-20 | 阅读：次

NSSCTF{}

Png

对于一个PNG文件来说，其文件头总是由位固定的字节来描述的，

.PNG

89 50 4E 47 0D 0A 1A 0A

标准的PNG文件结构

`.PNG` `IHDR` `IDAT` `IEND`

strings 扫描

strings 1.png

实例结果

C:\Users\86182\Downloads>strings 1.png
IHDR
IDATx
?{ S
?{ S
?,W%
777}
(NuS
?[!S
1Kf&
&RKN
UL~b
_sIMX
'O$^R
(NuS
o<}y
3I      X
$$?k
1k#xU
WxbXK<
oUyM~A
3f-c
qFQ:)
OLm-9
(NUK<1
/Ev7}U
L<{5
_sIMX
W]fp
a-cb
!fILN
oUyM~A
/Ev7}U
y/>]
&#+P
od/d
I       _3
I       _3
I       _3
I       _3
IEND

没什么信息

010editor

或者其他十六进制查看/编辑器

搜索{ 或者}

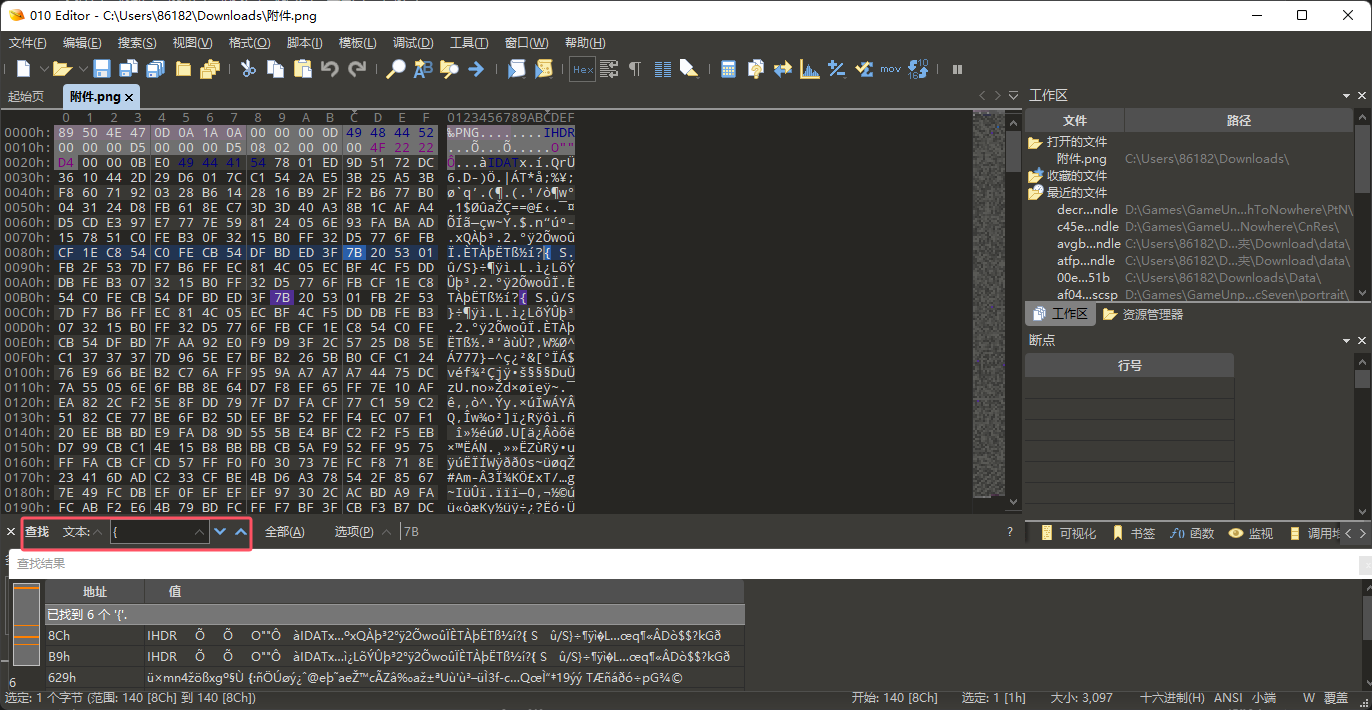
复制为十六进制文本

7B 20 53 01 FB 2F 53 7D
7B 20 53 01 FB 2F 53 7D
7B 35 8F 7D

pngcheck

pnggroup/pngcheck: Development of pngcheck 4

下载源码进入根目录cmd

cmake .
cmake --build . --config Release

使用实例

pngcheck 1.png
#OK: 1.png (213x213, 24-bit RGB, non-interlaced, static, 97.7%).

pngcheck -v 1.png
#File: 1.png (3097 bytes)
#  chunk IHDR at offset 0x0000c, length 13
#    213 x 213 image, 24-bit RGB, non-interlaced
#  chunk IDAT at offset 0x00025, length 3040
#    zlib: deflated, 32K window, superfast compression
#  chunk IEND at offset 0x00c11, length 0
#No errors detected in 1.png (3 chunks, 97.7% compression).

LSB隐写

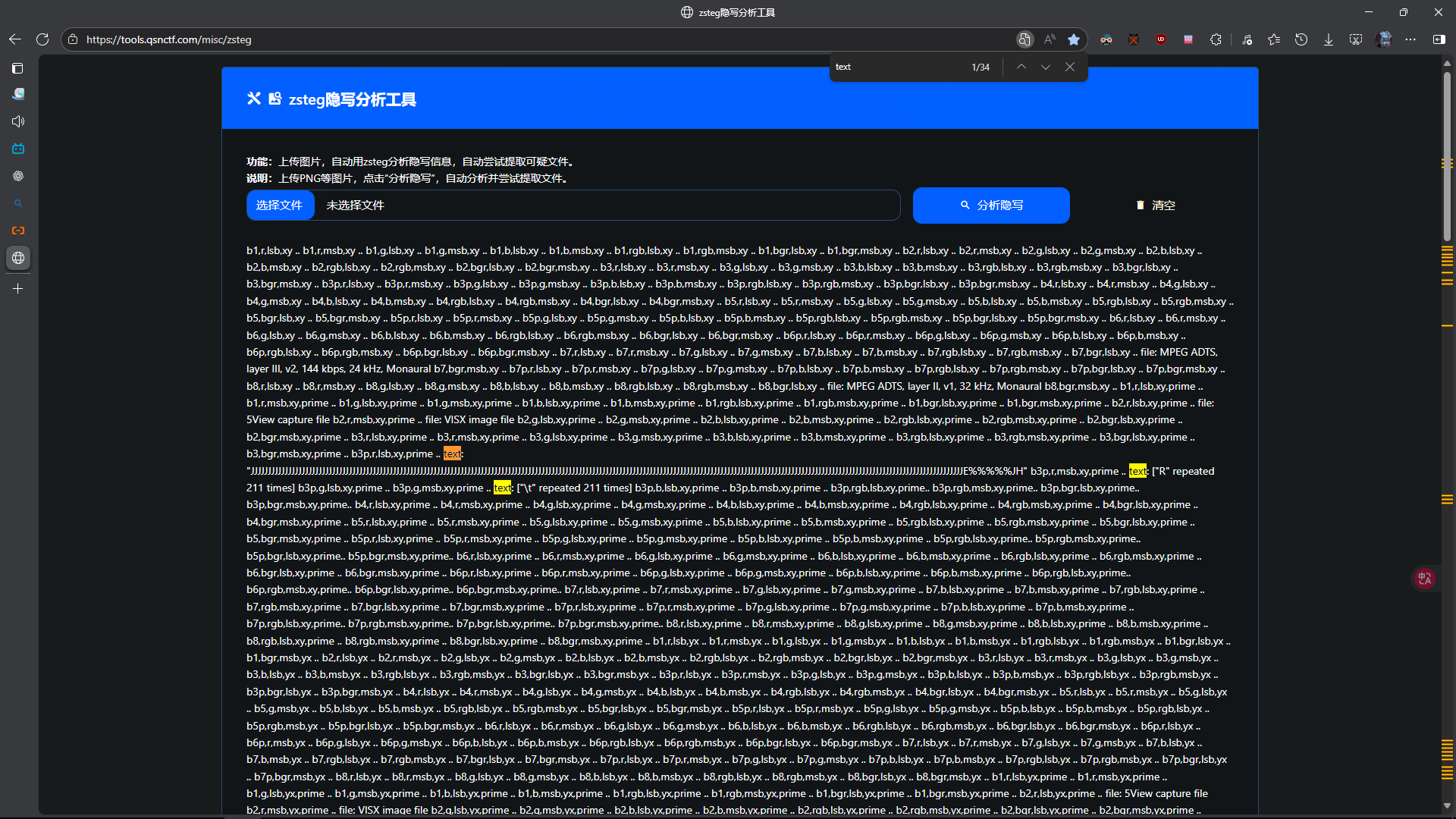
zsteg

zsteg隐写分析工具

搜索text {}相关

StegSolve

StegOnline

依次查看R G B为0时输出数据。

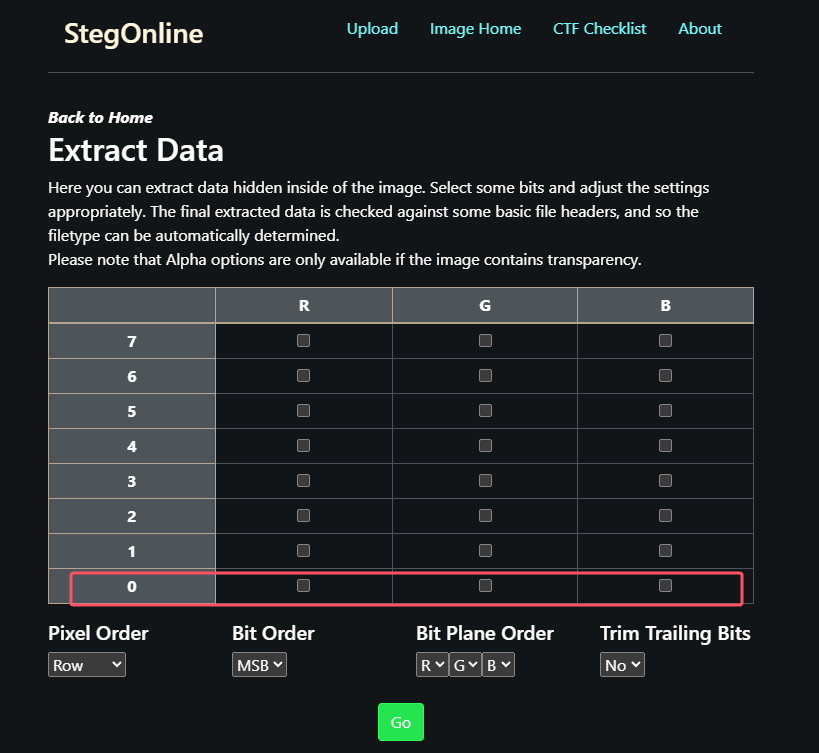
文本txt

词频分析

WebShell

工具

蚁剑源码

加载器启动器启动后需要初始化，选择源码根目录。

Fiddler打开的时候会修改SSL证书导致picgo图片上传失败。

BurpSuite

直接连接

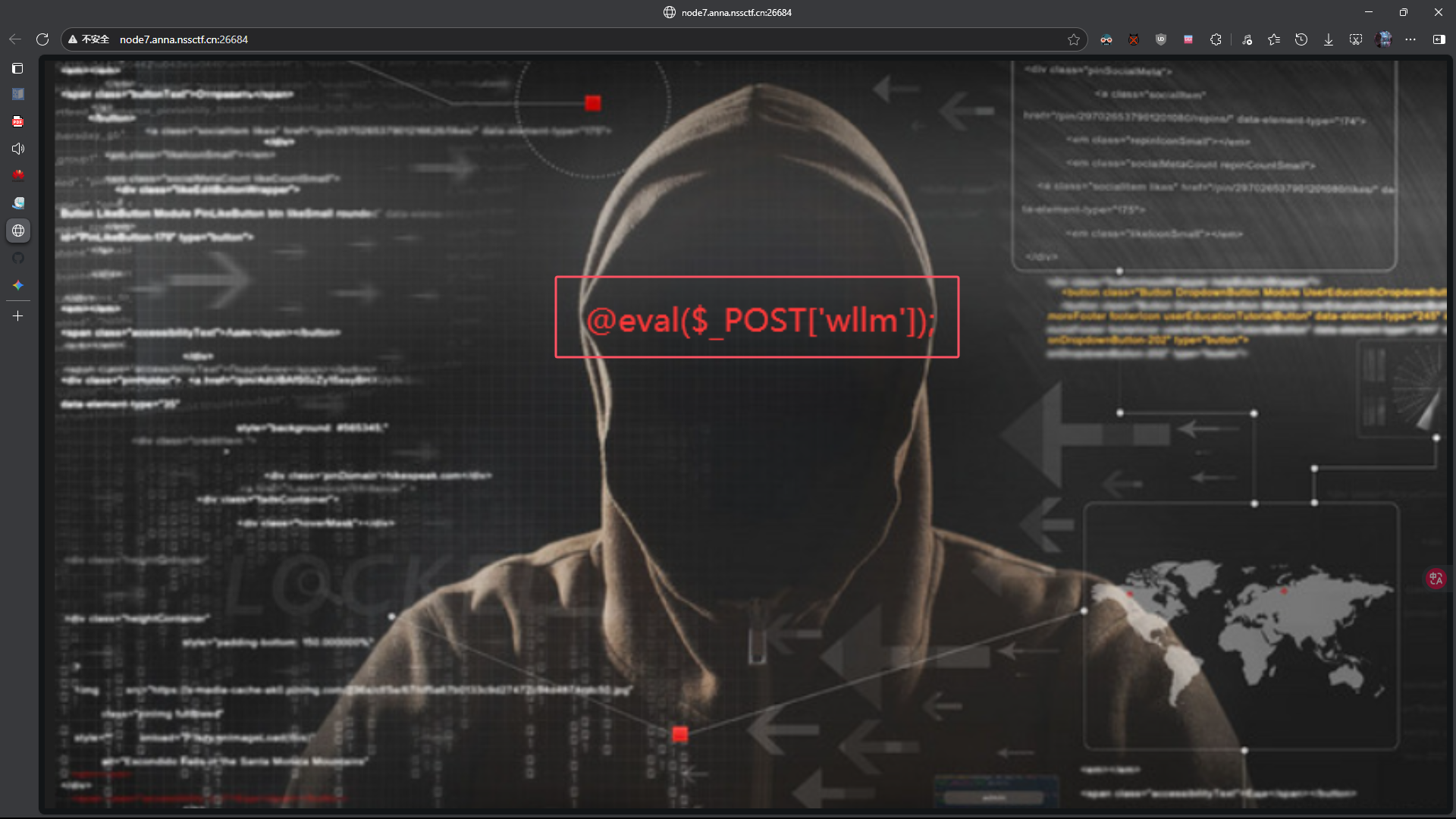
提示需要POST wllm，暗示webshell连接密码为wllm

使用蚁剑连接

手动查找flag，发现在顶层目录下。

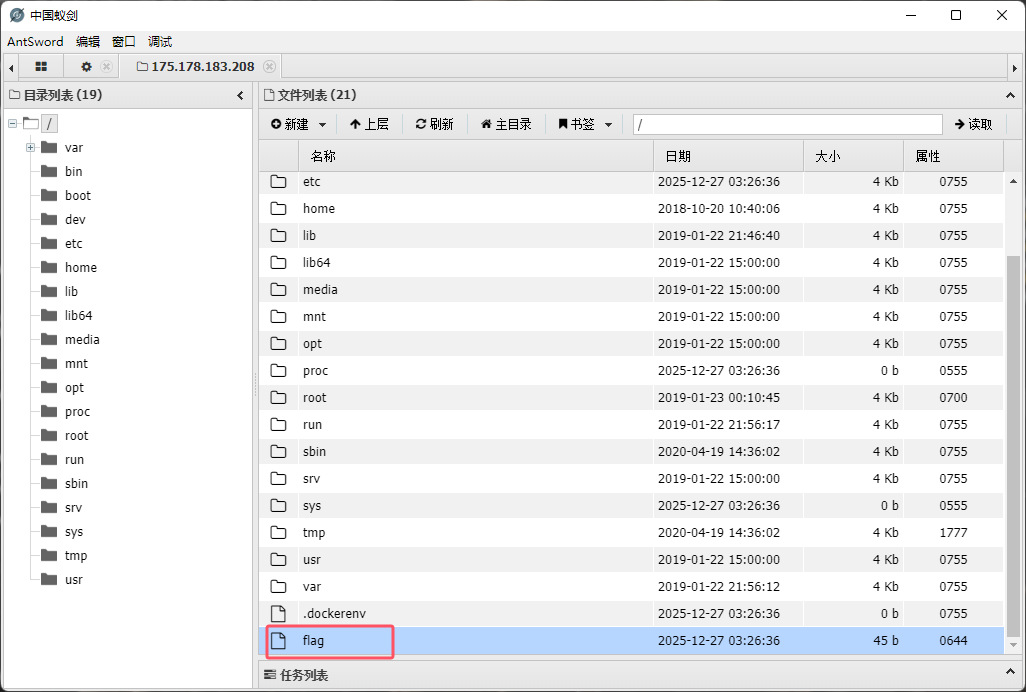
或者使用命令行搜索

find / -name "*flag*" 2>/dev/null

cat打印

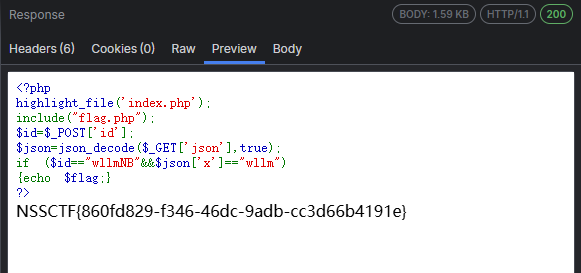
Payload

<?php
highlight_file('index.php');
include("flag.php");
$id=$_POST['id'];
$json=json_decode($_GET['json'],true);
if ($id=="wllmNB"&&$json['x']=="wllm")
{echo $flag;}
?>

提示需要发送POST 和 GET，需要满足id为wllmNB 以及 json['x']=="wllm"

打开fiddler，选择composer组件

URL，默认http1.1

http://node7.anna.nssctf.cn:27699/index.php

添加GET参数

转义工具URL 编码/解码 - 锤子在线工具

key: json 
value: {"x":"wllm"}
#注意这里需要使用转义字符
value: %7B%22x%22%3A%22wllm%22%7D

设置 Request Headers

Content-Type: application/x-www-form-urlencoded

填写 Request Body ，在body选择form-urlencoded

id=wllmNB

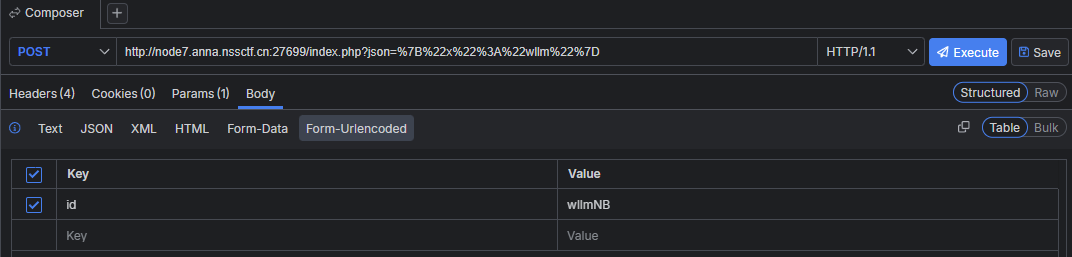
最后的结果为

POST http://node7.anna.nssctf.cn:27699/index.php?json=%7B%22x%22%3A%22wllm%22%7D HTTP/1.1
Host:node7.anna.nssctf.cn:27699
User-Agent:Fiddler-Everywhere
Content-Type:application/x-www-form-urlencoded
Content-Length:9

id=wllmNB

执行得到flag

加密/解密

工具

SageMath

SageMathInstallation Guide

在线工具Sage Cell Server，没有一些基础的库比如说crypto相关，导致无法使用long2bytes，需要手动转换一下

#Ubunbu参考WSL安装方法
#添加环境变量
nano ~/.bashrc
#根据安装目录调整，添加到尾部即可。
#export PATH="/home/wdream/Tools/miniforge3/bin:$PATH"
source ~/.bashrc
conda --version

Ciphey

cyphey命令行工具，需要python3.8.8安装，推荐使用anaconda

安装具体细节参考用Anaconda安装ciphey的过程记录 - 知乎

ciphey -t 4O595954494Q32515046324757595N534R52415653334357474R4N575955544R4O5N4Q46434S4O59474253464Q5N444R4Q51334557524O5N4S424944473542554O595N44534O324R49565746515532464O49345649564O464R4R494543504N35
ciphey -f encrypted.txt

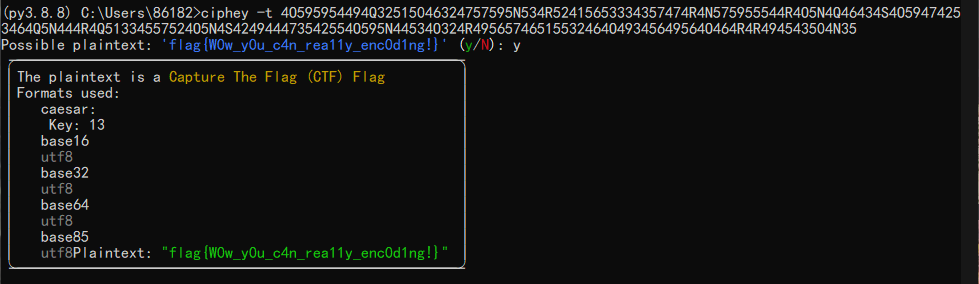
分析过程：

原密文

4O595954494Q32515046324757595N534R52415653334357474R4N575955544R4O5N4Q46434S4O59474253464Q5N444R4Q51334557524O5N4S424944473542554O595N44534O324R49565746515532464O49345649564O464R4R494543504N35

首先统计一下出现的字符集，0~9和NOQRS，字母数量特别少而且是相邻字符，疑似是偏移过的Base16

#!/usr/bin/env python3
import sys
from collections import Counter

def main():
    if len(sys.argv) < 2:
        print("用法: python count_chars.py <字符串>")
        sys.exit(1)

    input_str = sys.argv[1]  # 获取第一个参数作为输入字符串
    counts = Counter(input_str)  # 统计字符出现次数

    # 按字符排序输出
    for char in sorted(counts):
        print(f"'{char}': {counts[char]}")

if __name__ == "__main__":
    main()

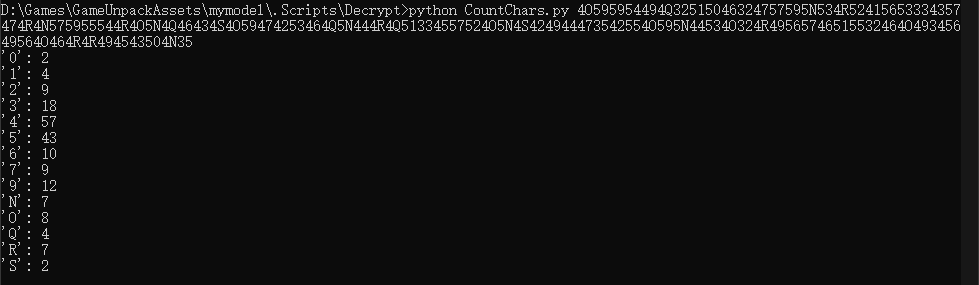
NOQRS对应偏移的ABDEF，如果是偏移的则offset = ‘N’ - ‘A’ = 78 - 65 = 13

caesar还原为

4B595954494D32515046324757595A534E52415653334357474E4A575955544E4B5A4D46434F4B59474253464D5A444E4D51334557524B5A4F424944473542554B595A44534B324E49565746515532464B49345649564B464E4E494543504A35

再使用Base16解密得到

KYYTIM2QPF2GWYZSNRAVS3CWGNJWYUTNKZMFCOKYGBSFMZDNMQ3EWRKZOBIDG5BUKYZDSK2NIVWFQU2FKI4VIVKFNNIECPJ5

分析字符集包括部分数字和大写字母，刚好符合Base32的字符集

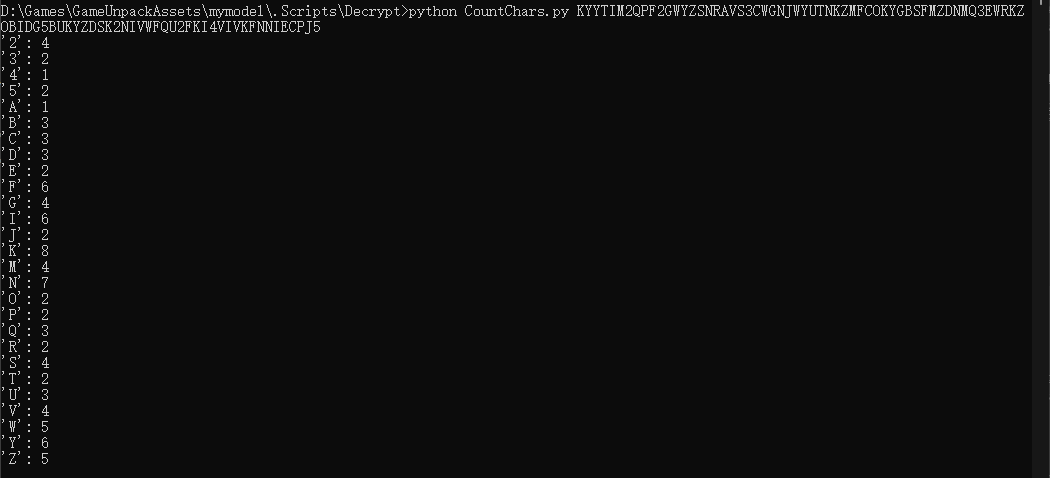
尝试使用Base32解密得到

V143Pytkc2lAYlV3SlRmVXQ9X0dVdmd6KEYpP3t4V29+MElXSER9TUEkPA==

结尾有两个=，直接猜测是Base64，进行解密得到

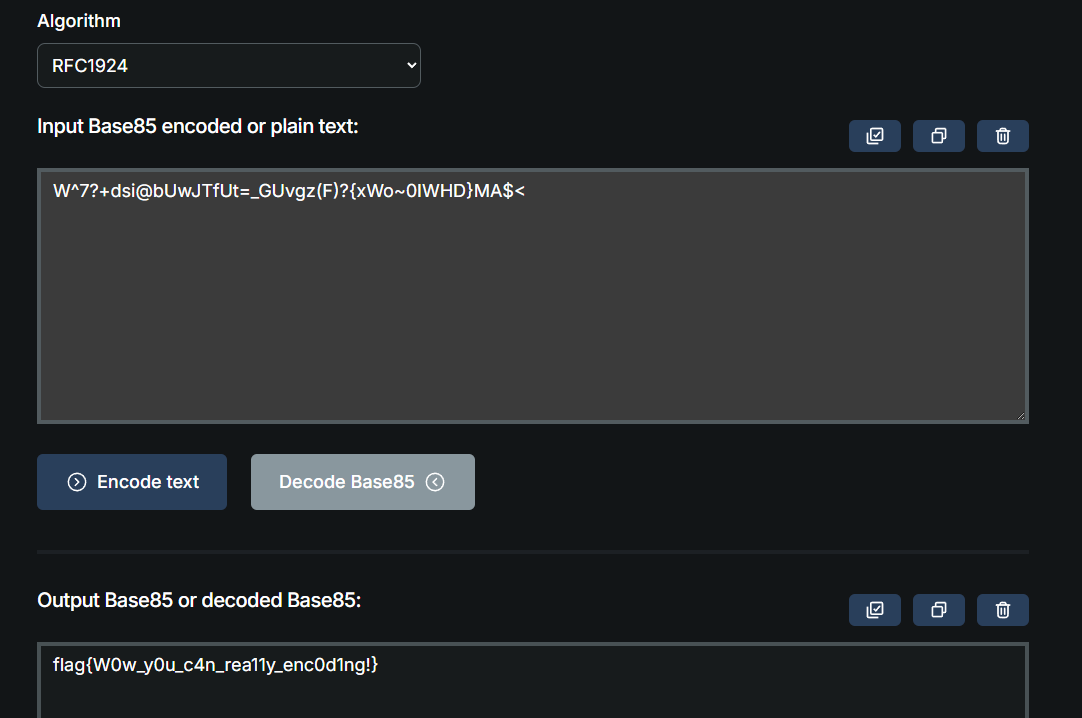
W^7?+dsi@bUwJTfUt=_GUvgz(F)?{xWo~0IWHD}MA$<

可以看到这里有很多特殊符号，猜测是Base85或者Base91

如果用91进行解密会直接得到乱码，肯定不正确。

��W*!��H���9��N$� � �xptr�R�`Nl�

但是如果用85进行解密，会提示开头不能是W，这里是因为大部分解密工具选择的算法不对。需要选择RFC1924算法。Base85 Encoder And Decoder

最后得到flag为

Caesar

偏移量

BaseX

X表示的是编码字符数量

Base16

0123456789ABCDEF

没有小写字母，特点只有6种大写字母

Base32

ABCDEFGHIJKLMNOPQRSTUVWXYZ234567

没有小写字母，只有部分数字，缺少数字0 1 8 9

Base58

123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz

没有0

Base62

0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz

Base64

ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/=

结尾一般有= 比较好辨别，有大小写数字。

Base85

有多种算法Base85 Encoder And Decoder

包括 Adobe, Ascii, RFC1924, Z85 等

Ascii85 标准（! 到 u）

!"#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_`abcdefghijklmnopqrstu

Z85（ZeroMQ 提出）：使用完全可打印的 85 个字符，不包括容易混淆的字符（如 "、\ 等）

有很多特殊符号

Base91

ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789!#$%&()*+,./:;<=>?@[]^_`{|}~"

包括数字，字母，符号，没有反斜杠\，单引号‘

对称加密算法

三对称加密算法 - 知乎

RC

Rivest Cipher

RC2

RC2是传统的一种对称分组加密算法，可作为DES算法的建议替代算法。其输入和输出都是64bit。秘钥长度是1byte到128byte。

RC4

RC4 算法使用一个变长的密钥（通常为 8 至 256 字节）来生成一个伪随机的密钥流，然后将该密钥流与原始数据进行异或运算以实现加密。

KSA（the Key-Scheduling Algorithm) 秘钥调度算法，使用密钥生成S-box 替换盒
PRGA (the Pseudo-Random Generation Algorithm) 伪随机生成算法，使用调度盒生成密钥流，然后通过XOR明文得到密文。

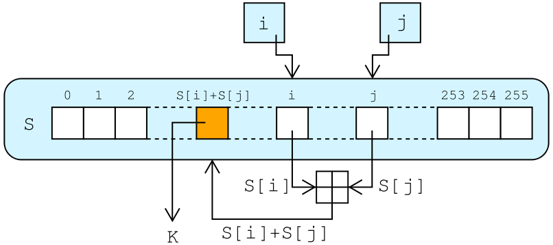
def rc4(key, data):
    S = list(range(256))
    j = 0
    out = []
    #KSA
    for i in range(256):
        j = (j + S[i] + key[i % len(key)]) & 0xFF
        S[i], S[j] = S[j], S[i]
    #PRGA
    i = j = 0
    for b in data:
        i = (i + 1) & 0xFF
        j = (j + S[i]) & 0xFF
        S[i], S[j] = S[j], S[i]
        out.append(b ^ S[(S[i] + S[j]) & 0xFF])
   
    return bytes(out)

TEA

Tiny Encryption Algorithm, 微型加密算法

算法	数据块
TEA	固定 64-bit（2×uint32）
XTEA	固定 64-bit
XXTEA	任意长度 uint32 数组

TEA $delta = \frac{\sqrt{5}-1}{2} *2^{32} = 0x9E3779B9$

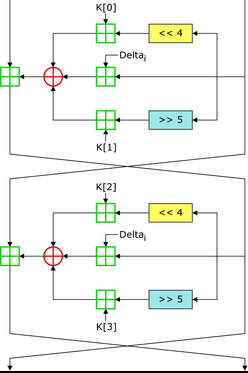
void TEA_Encrypt(long* EntryData, long* Key)
{
    //分别加密数组中的前四个字节与后4个字节,4个字节为一组每次加密两组
    unsigned long x = EntryData[0];
    unsigned long y = EntryData[1];
    
    unsigned long sum = 0;
    unsigned long delta = 0x9E3779B9;
    //总共加密32轮
    for (int i = 0; i < 32; i++)
    {
        sum += delta;
        x += ((y << 4) + Key[0]) ^ (y + sum) ^ ((y >> 5) + Key[1]);
        y += ((x << 4) + Key[2]) ^ (x + sum) ^ ((x >> 5) + Key[3]);
    }
    //最后加密的结果重新写入到数组中
    EntryData[0] = x;
    EntryData[1] = y;
}

腾讯的TEA只使用16轮次。

XTEA

XTEA是TEA的升级版，增加了更多的密钥表，移位和异或操作等，设计者是Roger Needham, David Wheeler，防止密钥表攻击。

之前的密钥是按照固定索引来使用的，现在就是通过定义新的计算来获取索引。

[原创]TEA、XTEA、XXTEA加解密过程及案例-密码应用-看雪安全社区｜专业技术交流与安全研究论坛

void XTEA_Encrypt(long* EntryData, long* Key)
{
    unsigned long x = EntryData[0];
    unsigned long y = EntryData[1];
   
    unsigned long sum = 0;
    unsigned long delta = 0x9E3779B9;
   
    for (int i = 0; i < 32; i++)
    {
        x += (((y << 4) ^ (y >> 5)) + y) ^ (sum + Key[sum & 3]);
        sum += delta;
        y += (((x << 4) ^ (x >> 5)) + x) ^ (sum + Key[(sum >> 11) & 3]);
    }
   
    EntryData[0] = x;
    EntryData[1] = y;
}

XXTEA

Corrected Block TEA

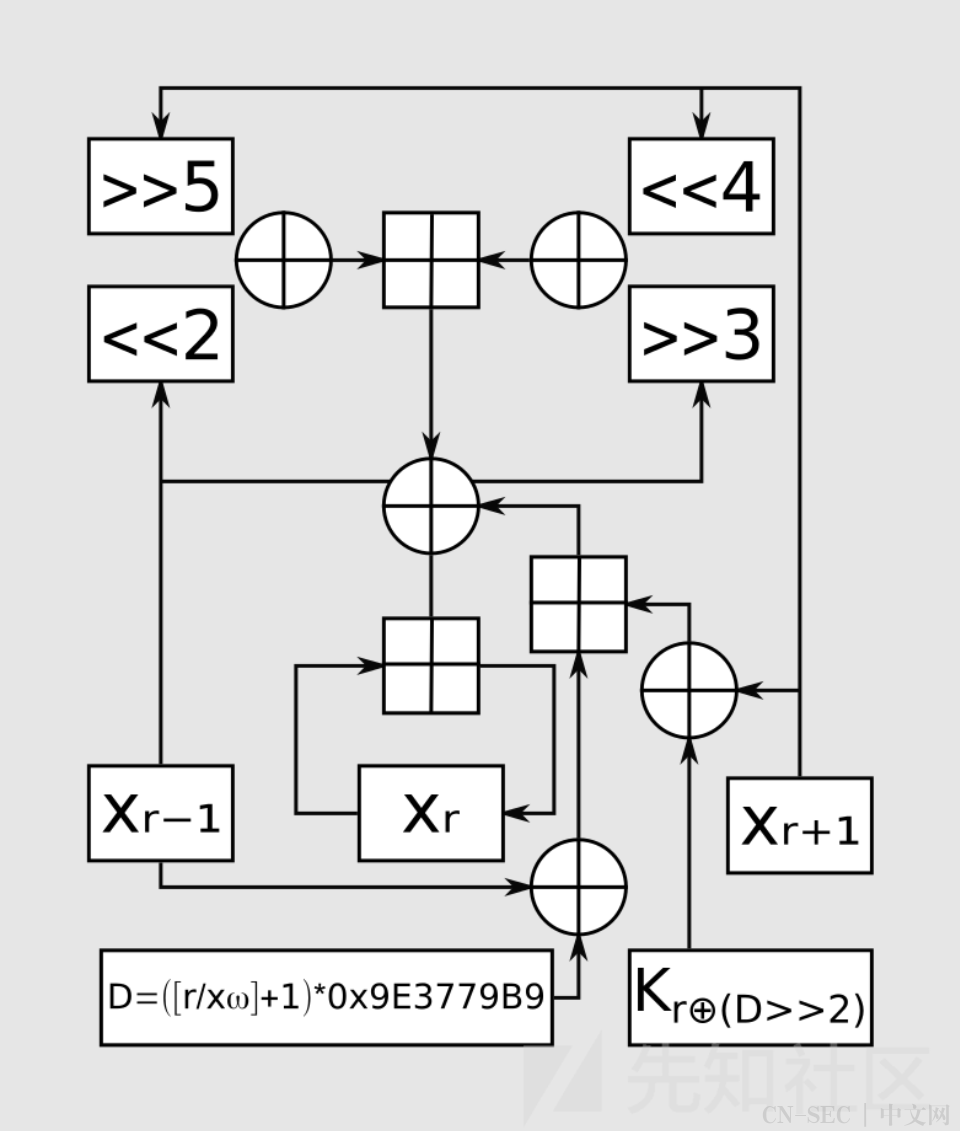
#define MX (((z >> 5) ^ (y << 2)) + ((y >> 3) ^ (z << 4))) ^ ((sum ^ y) + (key[(p & 3) ^ e] ^ z))
#数据 数据块数 密钥
void XXTEA_Encrypt(uint32_t* data, int n, const uint32_t key[4])
{
    if (n < 2) return;
   
    uint32_t y, z, sum = 0;
    uint32_t p, rounds, e;
   
    rounds = 6 + 52 / n;
    z = data[n - 1];
   
    while (rounds--)
    {
        sum += DELTA;
        e = (sum >> 2) & 3;
   
        for (p = 0; p < (uint32_t)(n - 1); p++)
        {
            y = data[p + 1];
            z = data[p] += MX;
        }
   
        y = data[0];
        z = data[n - 1] += MX;
    }
}

DES

Data Encryption Standard

分组长度：64 bit

密钥长度：64 bit（其中 56 bit 有效，8 bit 为奇偶校验）

结构：Feistel 网络

轮数：16 轮

DES 56-bit 密钥空间过小，已被淘汰

明文按 64 位分组，初始置换（IP）

进入 16 轮 Feistel 结构
- 右半部分扩展（32 → 48 bit）
- 与子密钥异或
- S 盒替换（非线性）
- P 置换
左右交换

逆初始置换（IP⁻¹）

输出密文
3DES

Triple DES是DES向AES过渡的加密算法，它使用2条56位的密钥对数据进行三次加密。是DES的一个更安全的变形。

AES

Advanced Encryption Standard, 高级加密标准

AES拥有三种不同的密钥长度抵抗蛮力攻击

AES	密钥长度（比特)	分组长度(比特)	向量长度(比特)	加密轮数
AES-128	128	128	128	10
AES-192	192	128	128	12
AES-256	256	128	128	14

只定义单块加密，需要配合分组工作模式使用，所以有AES-CBC, AES-CTR等。

FISH

TWOFISH

BLOWFISH

SM4

工作模式

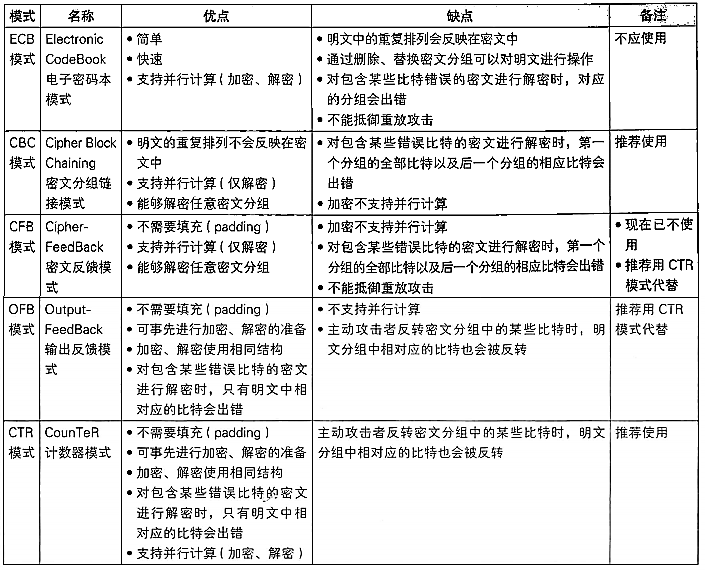
分组加密工作模式

ECB Electronic Codebook 不安全，每个分组分别加密后就是对应分组密文，解密不需要IV，与加密流程完全对称
CBC Cipher Block Chaining

第一组加密后的数据通过XOR IV得到第一组密文，后续每一组加密的数据都要XOR前一组加密的数据得到密文。
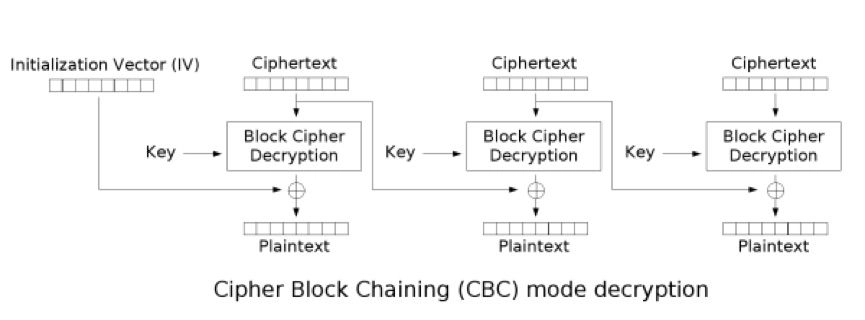
CTR Counter Mode

每个轮次的加密都会生成一个随机数Nounce值来初始化CTR

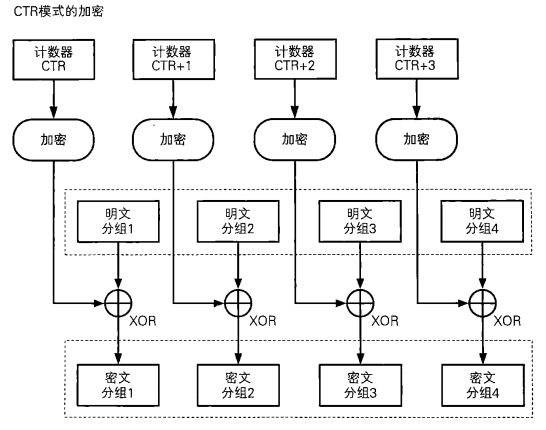![AES的CTR模式加密解密详解 Wuman’s Blog](https://cdn.jsdelivr.net/gh/violet-wdream/Drawio/PNG/202602042004575.png)
GCM Galois/Counter Mode

是一种将 加密与认证 合并的分组密码工作模式

结构：CTR + GHASH
1. CTR 模式加密数据
2. Galois 域哈希（GHASH）对数据做认证
3. 生成 认证标签（TAG）
```
明文 ──CTR(AES)──> 密文
  │
  └──AAD ──GHASH──> TAG
```
AAD：附加认证数据

TAG：认证标签（常见 128 bit）

填充Padding

当明文长度 不是分组密码块大小的整数倍 时，按规则补齐数据长度。

以 AES 为例：分组大小固定为 16 字节（128 bit）。

ECB 和 CBC需要Padding

PKCS#7 填充字节的值 = 填充字节数 ，比如缺了128位（16B）就在后面填16个0x10
ZERO 缺了填0
ANSI X.923 最后一个字节是填充长度前面补 0
ISO/IEC 7816-4 第一个填充字节是 0x80 后面补 0

非对称加密

RSA

RSA公开密钥密码体制的原理是：根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

选择两个大素数 p 和 q
计算： $n=p×q$ 这里 n 称为模数，它决定了密钥长度（通常 1024~4096 位）
计算欧拉函数： $ϕ(n)=(p−1)(q−1)$
选择公钥指数 e，满足： $1<e<ϕ(n),gcd(e,ϕ(n))=1$ gcd是最大公约数，公钥通常会给出。
计算私钥指数 d： $d≡e^{−1}(mod \spaceϕ(n))$

(mod ϕ(n))指的是同余，≡是约束关系而不是=，这里-1指的是模逆运算，等价于
\[\\d*e ≡1 \space (mod \spaceϕ(n)) \\=> \\(d*e) \space mod \spaceϕ(n)=1 \\=> d=inverse\_mod(e,\spaceϕ(n))\]

密钥类型	内容
公钥 (public key)	(n, e)
私钥 (private key)	(n, d)

加密与解密

加密（用公钥加密消息 m）：

\[c=m^e \space mod\space n \\\]

解密（用私钥还原消息 c）：

\[m=c^d\space mod\space n \\=>pow(c, d, n)\]

这里 m 要转为整数表示（通常用 bytes_to_long 转换）。

Coppersmith

Coppersmith是指泄露了一部分信息的RSA

PR.<x> = Zmod(n)[] #x是多项式自变量，Zmod(n)表示 多项式的系数是模n的
f = (p_base + (i << 265))  +  x * (mod << 6)
roots = f.monic().small_roots(X=2^453, beta=0.4, epsilon=0.05)
assert roots
p = f(roots[0])

X=2^453表示自变量x取值范围 $[0, 2^{453} - 1]$

beta和epsilon通常不动，epsilon越小表示探索深度越大，花费时间越多。

实例，求出flag

这里是公钥加密信息flag得到加密信息ct

p = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 65537
hint1 = p >> 724
hint2 = q % (2 ** 265)
ct = pow(bytes_to_long(flag), e, n)
print(hint1)
print(hint2)
print(n)
print(ct)

#1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
#40812438243894343296354573724131194431453023461572200856406939246297219541329623
#21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
#19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188

getPrime是生成指定位数的素数，这里的p q都是1024位的素数。

p >> 724：泄露了 p 的高 1024-724 = 300 位也就是hint1

q % 2^265：泄露了 q 的低 265 位也就是hint2

解密脚本，需要在SageMath环境下运行

from Crypto.Util.number import long_to_bytes
h1, h2 = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479, 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
c = 19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188
e = 65537
#h1是p的高300位（放在了低位），h2是q的低265位
# 1. 构造 p 的已知部分
mod = 1 << 265 #2^265
p_high = h1 << 724 #将高300位放到高位
#p = h1_724bit
#q = 759bit_h2
#n = p * q
#h2^-1 = inverse_mod(h2, 2^265)
#(n * h2^-1) % mod = (p % mod) * [(759bit_h2 * h2^-1) % mod] = (p % mod) * 1
p_low = (n * inverse_mod(h2, mod)) % mod #得到p的低265位
p_base = p_high + p_low #拼接p，中间有1024-300-265 = 459位缺失（265位~723位）

# 2. 使用 Coppersmith 算法查找 p 的中间缺失位
PR.<x> = Zmod(n)[] #x是多项式自变量，Zmod(n)表示 多项式的系数是模n的
for i in range(64):#2^6 = 64 爆破6位（穷举）
    # 构建多项式: f(x) = (p_base + i*2^265) + x*2^329 (2^329 = mod * 64)
    f = (p_base + (i << 265))  +  x * (mod << 6)
    #注意monic首一化
    roots = f.monic().small_roots(X=2^453, beta=0.4, epsilon =0.05) # 453 = 459 - 6 爆破了6位
    if roots:
        p = int(f(roots[0]))#需要强转int
        break
# 3. 解密 RSA
q = n // p
d = inverse_mod(e, (p - 1) * (q - 1))
print(long_to_bytes(pow(c, d, n)))

执行

sage rsa.py

flag{ef5e1582-8116-4f61-b458-f793dc03f2ff}

如果不手动爆破，即

#...
PR.<x> = Zmod(n)[]
f = p_base + x * mod
roots = f.monic().small_roots(X=2^459, beta=0.4, epsilon =0.04)
assert roots
p = int(f(roots[0]))
#...

epsilon收缩到0.04及以下均可。

Sage Cell Server 在线sage环境不能用long_to_bytes测试得到long56006392793429523039334991295440472601833419964063188654957241090275128167728784831578248304182847101本地转换为bytes

python -c "from Crypto.Util.number import long_to_bytes
print(long_to_bytes(56006392793429523039334991295440472601833419964063188654957241090275128167728784831578248304182847101))"

同样得到flag{ef5e1582-8116-4f61-b458-f793dc03f2ff}

Hastad 广播攻击

CRT中国剩余定理 China Remainder Theorem中国剩余定理 - OI Wiki

「物不知数」问题：有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

解方程组

得到最小非负整数解$X = x + kN, N=Π^n_{i=1} n_i$

实例

# FLAG = bytes_to_long(pad(b"flag{??????}",64))
# def init_key():
#     p, q = getPrime(512), getPrime(512)
#     n = p*q
#     e = 9
#     while(GCD((p-1)*(q-1),e)!=1):
#         p, q = getPrime(512), getPrime(512)
#         n = p*q
#     d = inverse(e,(p-1)*(q-1))
#     return n,e,d

# n_list=list()
# c_list=list()
# for i in range(9):
#     N,e,d=init_key()
#     n_list.append(N)
#     c=pow(FLAG,e,N)
#     c_list.append(pow(FLAG,e,N))
#     assert(pow(c,d,N)==FLAG)
# print("n_list:",n_list)
# print("c_list:",c_list)

p q都是512bit，n是1024bit，e = 9

后面的部分大致意思就是生成了9组模数n，一共用明文FLAG生成了9组密文c

所以已知c，e，n，记FLAG 为 m，记$N =Π^8_{i=0} n_i$

$$ \c_i = m^e\mod n_i \=> m^e ≡ c_i (\mod n_i)

\m = c^d_i \mod n_i \ \space=> m < n_i => m^9 < N $$ $m^e ≡ c_i (\mod n_i)$可以使用CRT中国剩余定理

crt(c_list, n_list)得到最小非负整数解M，M满足$M ≡ m^e (\mod N)$

但是m^e^ = m^9^ < N 所以m^e^ = M = crt(c_list, n_list)

再开e次根号得到m，也就是9次。

from Crypto.Util.number import long_to_bytes
n_list = [
]

c_list = [
]
e = 9
# CRT 合并
M = crt(c_list, n_list)
# 整数 9 次方根
m = M.nth_root(e)
print(long_to_bytes(int(m)))

Png