img

(❁´◡`❁)

Violet_Wdream

Personal Website

生如不定流水, 夕拾难觅朝花

计算机系统基础ICS 第二章习题讲解

| 阅读：次

目录

image-20241227110324127

必考

2^15 32768
2^16 65536
2^31 214748 3648
2^32 429496 7296
1010 A 10
1011 B 11
1100 C 12
1101 D 13
1110 E 14
IEEE 754float范围 ±[2^-126^ ， (2-2^-23^)*2^127^ ]

IEEE 754 规定移码全1(NaN)和全0(INFINITY)为特殊用途，所以 移码范围[1,254]

bias = 127; 移码8位1~254;

最大正数1.111 1111 1111 1111 1111 1111 * 2^254-127^ = (2-2^-23^)*2^127^;

最小正数1.000 0000 0000 0000 0000 0000* 2^-1-127^ = 2^-126^;

负数部分对称；

image-20241226230704925

float : 1+ 8+23 = 符号位 + 移码 + 小数 ； 偏置常数：127 =； 移码= 阶码（指数） + 偏置常数；

IEEE754规定, 当指数位全部为0或者全部为1时, 用于表示两种特殊状态的数: subnormal number 和 non-number

±1.1 float

整数部分: 1

小数部分：0.1 = 0.00 0110 0110 0110…

规格化: 1.00 0110 0110 0110 * 2^0

移码: 0+127 =0111 1111; 偏置常数127 阶码（指数） ： 0

小数:00 0110 0110 0110 0110 0110 1（110 ) 0舍1入

符号位：0

最后结果 ：

0 011 1111 1 00 0 110 0 110 0 110 0 110 0 110 1 ;
=3 F 8 C C C C D 
=3F8CCCCD H

0.2 0

0.4 0

0.8 0

1.6 1

1.2 1

0.4 0

0.8 0

1.6 1

±3.3 float

整数部分：11 ；

符号位：0：

小数部分：0.3 =0.0 1001 1001 1001 1001 …

11.0 1001 1001 1001 1001… = 1.10 1001 1001 1001 1001 1001 1 (001) * 2^1

符号位：0；

移码： 1 + 127 = 128 = 1000 0000

小数: 101 0011 0011 0011 0011 001 1

最终结果：0 100 0 000 0 101 0011 0011 0011 0011 0011
= 40533333 H

0.6 0 乘一次开始算

1.2 1

0.4 0

0.8 0

1.6 1

1.2 1

0.4 0

0.8 0

1.3 1

image-20241012161619392

image-20241012161610699

image-20241012155333114

178 = 128 + 32 + 16 +2 = 1000 0000 + 0010 0000 + 0001 0000 +0000 0010
    =1011 0010
    
0.125 = 1/8 =2^-3 = 0.001;
178.125 = 10110010.001

0 0111 1110 101 1000 0000 0000 0000 0000= +1.1011 * 2^-1 = 0.11011;
符号位:0;
移码：126 ; 指数（阶码）：126 - 127 =-1 ;
小数:.1011

9

image-20241216170939489

int x = -32768 ;//32768 = 2^15  65566 = 2^16
=-000...1000 0000 0000 0000 = 111..1000 0000 0000 0000 = FFFF8000 H;
short y  = 522 = 512 + 8+ 2 = 0000 0010 0000 1010 = 020A H;
unsigned z = 65530 = 65536-1 - 5 = 1111 1111 1111 1010 = 0000 FFFA H
char c = '@' = ???;不考 //@ 的ASCII码为40H 
float a = -1.1 = BF8CCCCD H // 1.1 = 3F8CCCCD H; 3.3 = 40533333 H; -3.3 = C0533333 H
double 不考// 1 + 11 + 52  移码：2^10 -1 =1023；

10

image-20241216170952949

int x = FFFF 0006 H；有符号数；= - 0000 FFFA H =- (2^16-1 -5) = - 65530;
short y = DFFC H = 1101 1111 1111 1100 = - 0010 0000 0000 0100 
    = -2^13 - 4 = -8092 -4 = -8096;
unsigned z = FFFF FFFA H = 2^32 -1 - 5 = 2147483648 - 6 = 2147483642;
char c = 2A H = 0010 1010 = 32 + 8 +2 = 42;
float a = C448 0000H = 1100 0100 0100 1000 0000 0000 0000 0000
    = 1 10001000 10010000000000000000000;//128+8-127 = 9
    = - 1.1001* 2^9;
double 不考

18

image-20241216170918044

因为strlen 返回的类型是一个 unsigned int ， 所以 strlen(str1) - strlen(str2) 的值也是unsigned int ，一定会大于等于0，所以如果strlen(str1)<strlen(str2) 返回值还是一个正数，导致返回的结果不正确。
修改为：return strlen(str1) > strlen(str2) ;  //这样返回的就是一个bool值，转为int就是0/1

21

image-20241216171223043

image-20241216171236089

arith : return x*M + y/N;//注意y/N可能发生取整；
optarith: 
if y<0 , return (x<<4 - x) + (y+3)>>2;//符号位1，右移填充1， N=4；+3是修正
else return (x<<4 - x) + y>>2;// M=15

image-20241227112552626

22

image-20241216171303534

（6）

image-20241227121832621

1位符号位； 8位阶码0~255； 23位尾数；偏置常数128

如果阶码全1 （255） 或者全0（0）不用，则阶码范围1~254

但是只有IEEE754约定了会这么做，这里我们考虑阶码范围0~255

1.111 1111 1111 1111 1111 1111 * 2^255-128^ = (2-2^-23^)*2^127^ = (1-2^-24^)*2^128^

1.000 0000 0000 0000 0000 0000 * 2^0-128^ = 2^-128^;

答案错了

image-20241227121209298

16位移码定点整数通常使用0x8000（32768）作为偏移量，将原本[-32768, +32767]的范围平移到[0x0000, 0xFFFF]区间。解码时再减去0x8000即可还原到[-32768, +32767]。

16位补码定点整数 就是short

在 IEEE 754 浮点数中，基数通常是2(指2进制)，指数部分以一个偏置常数（Bias）进行存储。 • 单精度（32 位）偏置常数为127 • 双精度（64 位）偏置常数为1023

unsigned short 0~2^16-1 = 0~65535
16位原码定点小数1个符号位，15个小数位，原码 1 111 1111 1111 1111 = - (1- 2^-15) ~ 0 111 1111 1111 1111 = 1-2^-15
16位移码定点整数 -32768 ~ 32767
16位补码定点整数 (short) -32768 ~ 32767
阶码8位 ；7位尾数 ； 偏置常数 128 ±[ 2^-128^ ,(2-2^-7^)* 2^127^ ]

1.1111111 = (2-2^-7^)* 2^255-128^ = (2-2^-7^)* 2^127^;

1.0000000= 1* 2^0-128^ = 2^-128^;

23

image-20241216171316461

IEEE 754; 1+8+23
+1.75 :
符号位0，0.75转二进制：0.11 ； 1.75=1.11*2^0 ; 移码：0+127 = 127 ；尾数：.110 0000 ...
    0011 1111 1110 0000 0000 0000 0000 0000 = 3FE00000 H
    1.5 1
    1.0 1
    0.0 0
    ...;
+19 = 16+2+1 = 10011.0 = 1.0011 * 2^4;  4+127 = 131 = 1000 0011
0 1000 0011 001 1000 0000 0000 0000 0000 = 
    0100 0001 1001 1000 0000 0000 0000 0000 = 4198 0000 H;
-0.125 = 0.001 = 1.0*2^-3;  -3 +127 =2^7 - 1 -3 = 0111 1100
符号位1
1 0111 1100 000 0000 0000 0000 0000 0000 = 
    1011 1110 0000 0000 0000 0000 0000 0000 = BE00 0000 H;
258 = 256 + 2 =1 0000 0010 = 1.0000001 *2^8; 8+127 = 1000 0111 
0 1000 0111 000 0001 0000 0000 0000 0000 = 
    0100 0011 1000 0001 0000 0000 0000 0000 =43810000 H

24

image-20241216171419823

4098 = 4096 +2 = 2^12 +2 = 00....1 0000 0000 0010 =00001002 H;

IEEE 754 : 符号位0 ， 1 0000 0000 0010 = 1.00000000001*2^12; 
移码12+127 = 128 +11 = 1000 1011;
尾数：000 0000 0001 0000 0000 0000 ;
0 1000 1011 000 0000 0001 0000 0000 0000;
0100 0101 1000 0000 0001 0000 0000 0000 
    = 45801000 H

    00000000001 序列完全相同，规格化后的尾数部分

28

image-20241216171432845

float x y;
short i;
x= -0.125; y =7.5 ; i =100;
x： 符号位1 ； 0.001 = 1.0*2^-3 移码 -3 +127 = 0111 1100 ;
1 0111 1100 001 0000 0000 0000 0000 0000；
    = 1011 1110 0000 0000 0000 0000 0000 0000；
    = BE 00 00 00 H ;
y: 符号位0 ; 111.1 = 1.111 * 2^2; 移码2 +127 = 128 +1 = 1000 0001 ;
0 1000 0001 111 0000 0000 0000 0000 0000;
=0100 0000 1111 0000 0000 0000 0000 0000;
=40 F0 00 00 H;
i: 符号位0：  64+32+4 = 0110 0100 = 00 64 H ;
地址 大端机器/H 小端机器/H
100 BE 00
101 00 00
102 00 00
103 00 BE
108 40 00
109 F0 00
110 00 F0
111 00 40
112 00 64
113 64 00

29

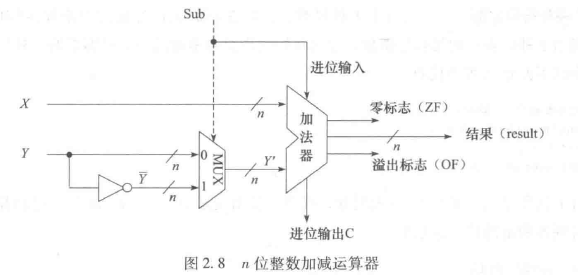
image-20241227160123086

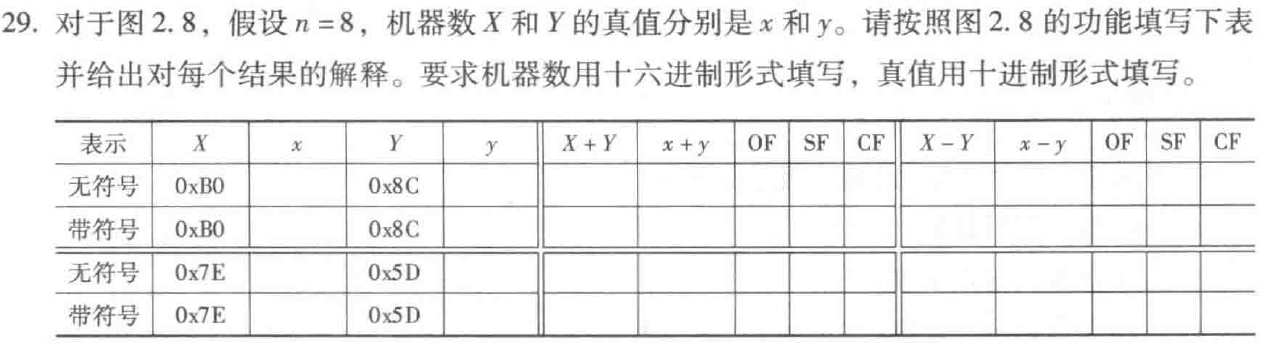
image-20241216171447753

表示 X x Y y X+Y x+y OF SF CF X-Y x-y OF SF CF
无符号 0xB0 176 0x8C 140 0x3C 60 1 0 1 0x24 36 0 0 0
带符号 0xB0 -80 0x8C -116 0x3C 60 1 0 1 0x24 36 0 0 0
                             
无符号 0x7E 126 0x5D 93 0xDB 219 1 1 0 0x21 33 0 0 0
带符号 0x7E 126 0x5D 93 0xDB -37 1 1 0 0x21 33 0 0 0

SF看结果是否符号位为1；

OF：操作数视作有符号数时结果溢出；

CF：操作数视为无符号数时结果溢出。CF溢出则OF必溢出

31

image-20241227161436799

image-20241216171512945

image-20241227161642229

int copy_array(int *array, int count){
    int I;
    /*在堆区申请一块内存*/
    unsigned long long arraysize=count* (unsigned long long) sizeof(int);
    
    //防止arraysize超过size_t 的范围导致溢出
    size_t myarraysize=(size_t) arraysize;
    if (myarraysize!=arraysize)
        return -1;
    
    int *myarray=(int *) malloc(myarraysize);
    
    
    if (myarray=NULL)
        return -1
        for (i=0;i<count; i++)
            myarray[i]=array[i];
    return count;
}

34

image-20241216171532407

ux = |x|; uy = |y|;int x, y;
x*x >=0 ; 假设x = 2^20, x*y会发生上溢后变成负数;非永真
(x-1<0)||x>0; x = -2^31 <0 ;x-1= 2*31-1>0 ; 非永真;
x<0 || -x <=0; 永真;
x>0 || -x >=0; x = -2^31 <0 ,-x = 2^31 = -2^31 < 0; 非永真;
（x& 0xf!=15） || (x<<28) <0 ;==> 若认为 ：x的低4位不是全1 or 第4位为1 ；则是永真；
    但是& 的优先级比！=更低, x & 0 ==0  ||(x<<28)<0 ;非永真;
x>y == -x< -y ; x = -2147483648 -x = -2147483648 ; if -x < -y , y=1; x<y 非永真;
~x + ~y ==~(x+y); x= 111111...111 = -1 ,~x =0; y=-1,~y =0; ~(x+y) =-1;非永真;

(int) (ux-uy) == -(y-x); ux - uy结果为unsigned ->int ; -(y-x) =x-y ->int;永真;

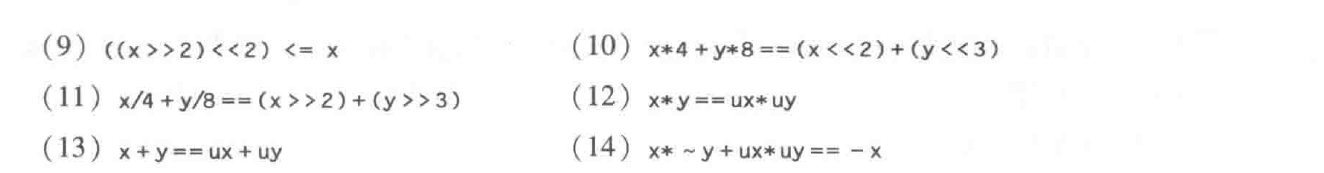
image-20241216171542749

(x >>2 )<<2 相当于把低2位置0，对于负数或者正数，都会变小/不变； 永真;
x*4 + y*8 ==(x<<2) + (y<<3); 永真 ;左移就是乘法;右移不完全是除法;
x/4+y/8 == x>>2 + y>>2; 非永真 ; x=-1, x/4 =0;x>>2 = -1;
x*y == ux*uy ;   非永真 if x*y <0 , ux * uy >=0 

x+y = ux + uy; 永真;
//int -> unsigned 并没有改变机器数；
x*~y + ux*uy == -x; => x*~y + x*y ==-x;  => x*(y+~y); -y=~y+1; y+~y=-1; 永真；

35

image-20241216171558185

dx * dx >=0 无论是否溢出，符号位单独运算（异或），0； 永真;
double(float)x 转可能float会发生舍入,不如直接转double精确；非永真;
dx + dy == (double)(x+y); x+y可能溢出;dx + dy 不会；非永真;
(dx + dy) + dz ==dx + (dy + dz) 永真;
dx * dy *dz ==dz * dy *dx ;乘积顺序会影响舍入 ;非永真;
dx/dx == dy/dy;if dx or dy =0  ; 非永真

41

image-20241216171617593

image-20241216171653369

1

float_bits float_abs(float_bits f) {
    unsigned sign=f>>31; //符号位
    unsigned exp=f>>23&0xFF; //阶码
    unsigned frac=f&0x7FFFFF; //尾数
    if （(exp==0xFF) && (frac!=0) ）    /*f为NaN*/
        return f;
    else
        return f&0x7FFFFFFF;               /*f为负数,符号位置0*/
}

2

float_bits float_neg(float_bits f) {
    unsigned exp=f>>23&0xFF;
    unsigned frac=f&0x7FFFFF;
    if (exp==0xFF) && (frac!=0)       /*f为NaN*/
        return f;
    else
        return f^0x80000000;          /* ^是按位异或，相当于取反符号位*/
}

3

float_bits float_half(float_bits f) {
    unsigned sign=f>>31;
    unsigned exp=f>>23&0xFF;
    unsigned frac=f&0x7FFFFF;
    //移码全1尾数全0： ∞；移码全1尾数不全0：NaN ；
    //移码全0，尾数全0：0；移码全0，尾数不为0：非规格浮点数；
    //规格化：exp + 127
    if (exp==0xFF) && (frac!=0)     /*f为NaN*/
        return f;
    else if（ ((exp==0)||(exp==0xFF)) && (frac==0) ）  /*f为0或∞ */
        return f ;
    else if （(exp==0) && (frac!=0)）              /*移码为0，f为非规格化数*/
        return sign<<31 | frac>>1; //sign置于最高位，拼接 对应段
    else {                                          /*f为规格化数*/
        exp=exp+0xFF;//移码 = 阶码 + bias 127
        if (exp!=0)                    /*0.5f为规格化数*/
            return sign<<31| exp<<23 | frac;
        else                              /*0.5f为非规格化数*/
            return sign<<31|  (frac | 0x800000)>>1;  
    }           
}

4

float_bits float_twice(float_bits f) {
    unsigned sign=f>>31;
    unsigned exp=f>>23&0xFF;
    unsigned frac=f&0x7FFFFF;
    
    if (exp==0xFF) && (frac!=0)     /*f为NaN*/
        return f;
    else if  ((exp==0)||(exp==0xFF)) && (frac==0)   /*f为0或∞ */
        return f ;
    else if (exp==0) && (frac!=0) {             /*f为非规格化数*/
        if (frac&0x400000)               /*f的尾数第一位为1*/
            return sign<<31 | 1<<23 | (frac&0x3FFFFF)<<1;
        else                                         /*f的尾数第一位为0*/
            return sign<<31 | frac <<1; 
        return sign<<31| frac>>1;
    }
    else {                                          /*f为规格化数*/
        exp=exp+0x01;
        if (exp!=0xFF)                    /*2.0f为规格化数*/
            return sign<<31| exp<<23 | frac;
        else                              /*2.0f为非规格化数*/
            return sign<<31| exp<<23 ;  
    }           
}

5

float_bits float_ i2f(int i) {
    unsigned pre_count=30;
    unsigned sign=(unsigned) i>>31;
    unsigned neg_i;
    if (i==0)     /*i为0*/
        return i;
    if (sign==0) {                      /*i为正数*/
        while (i>>pre_count ==0) pre_count--;
        return sign<<31 | (127+pre_count) <<23 | (unsigned)(i<<(32-pre_count))>>23;
    }
    else   {                                /*i为负数*/
        while (i<<pos_count==0) pos_count--;
        neg_i=(~(i>>(32-pos_count)) <<(32-pos_count)) |(1<<(31-pos_count));
        while (neg_i>>pre_count ==0) pre_count__;
        return sign<<31 |(127+pre_count)<<23 | neg_i<<(32-pre_count) >>23;
    }
}

6

int float_ f2i(float_bits f) {
    unsigned sign=f>>31;
    unsigned exp=f>>23 & 0xFF;
    unsigned frac=f&0x7FFFFF;
    unsigned exp_value=exp -127;
    unsigned neg_i;
    unsigned pos_count=31;
    if ((exp==0xFF) || (exp_value>30))     /*f为NaN或∞或值太大*/
        return 0x80000000;
    else if  ((exp==0) || (exp_value<0))        /* f为非规格化数或0或值太小*/
        return  0；
    else if (sign==0)                                 /* f为正的规格化数*/
        return (1<<30| (frac<<7)>>(30-exp_value); 
    else{                        /* f为负的规格化数*/                                
        neg_i=(1<<30 | (frac<<7) >>(30-exp_value);
        while (neg_i<<pos_count==0) pos_count--;
        return (~(neg_i>>(32-pos_count))<<(32-pos_count)) |(1<<(31-pos_count));
    } 
}

Comments